12.5 The Cross Product
This section introduces the cross product \(\textbf{v}\times w\) of two vectors \(\textbf{v}\) and \(\textbf{w}\). The cross product (sometimes called the vector product) is used in physics and engineering to describe quantities involving rotation, such as torque and angular momentum. In electromagnetic theory, magnetic forces are described using cross products (Figure 12.48 and Figure 12.49).
Unlike the dot product \(\textbf{v} \cdot w\) (which is a scalar), the cross product \(\textbf{v}\times w\) is again a vector. It is defined using determinants, which we now define in the \(2\times 2\) and \(3\times 3\) cases. A \(2\times 2\) determinant is a number formed from an array of numbers with two rows and two columns (called a matrix) according to the formula \begin{equation} \boxed{ \left| \begin{array}{cc} a & b \\ c& d \\ \end{array} \right| = ad - bc }\tag{1} \end{equation}

Note that the determinant is the difference of the diagonal products. For example, \[ \left| \begin{array}{cc} 3& 2 \\ \frac12 & 4 \\ \end{array} \right| = \left|\begin{array}{cc} \psline 3 & 2 \\ \frac12 & 4 \end{array}\right|\hspace{.2cm} - \hspace{.2cm} \left|\begin{array}{cc} 3 & \psline 2 \\ \frac12 & 4 \end{array}\right| = 3\cdot 4 - 2\cdot\frac12 = 11 \]
The determinant of a \(3\times 3\) matrix is defined by the formula \begin{equation} \boxed{ \left| \begin{array}{ccc} a_1 & b_1&c_1 \\ a_2 & b_2&c_2 \\ a_3 & b_3&c_3 \\ \end{array} \right| = a_1 \underset{\textrm{\((1,1)\)-minor}}{\left| \begin{array}{cc} b_2 & c_2 \\ b_3 & c_3 \\ \end{array} \right|} -b_1\underset{\textrm{\((1,2)\)-minor}}{\left| \begin{array}{cc} a_2 & c_2 \\ a_3 & c_3 \\ \end{array} \right|} + c_1\underset{\textrm{\((1,3)\)-minor}}{\left| \begin{array}{cc} a_2 & b_2 \\ a_3 & b_3 \\ \end{array} \right|}}\tag{2} \end{equation}
This formula expresses the \(3\times 3\) determinant in terms of \(2\times 2\) determinants called minors. The minors are obtained by crossing out the first row and one of the three columns of the \(3\times 3\) matrix. For example, the minor labeled \((1,2)\) above is obtained as follows: \[ \underset{\textrm{Cross out row 1 and column 2}}{\left| \begin{array}{ccc} \pnode a_1 & \smash{\pscirclebox {b_1}}&c_1\pnode \ncline \\ a_2 & b_2&c_2 \\ a_3& \psline b_3&c_3\\ \end{array} \right|} \qquad\textrm{to obtain the \((1,2)\)-minor}\qquad \underset{\textrm{(1,2)-minor}}{\left| \begin{array}{cc} a_2 & c_2 \\ a_3 & c_3 \\ \end{array} \right|} \]
Note
The theory of matrices and determinants is part of linear algebra, a subject of great importance throughout mathematics. In this section, we discuss just a few basic definitions and facts needed for our treatment of multivariable calculus.
EXAMPLE 1 A \(3\times 3\) Determinant
Calculate \(\quad { \left| \begin{array}{ccc} 2 & 4 & 3 \\ 0 & 1 & -7 \\ -1 & 5 & 3 \\ \end{array} \right|}\).
Solution \begin{align*} \left| \begin{array}{ccc} \smash{\pscirclebox{2}} & \smash{\pscirclebox{4}} & \smash{\pscirclebox{3}} \\ 0 & 1 & -7 \\ -1 & 5 & 3 \\ \end{array} \right| &= \pscirclebox{2}\left| \begin{array}{cc} 1 & -7 \\ 5 & 3 \\ \end{array} \right| -\pscirclebox{4}\left| \begin{array}{cc} 0 & -7 \\ -1 & 3 \\ \end{array} \right| + \pscirclebox{3}\left| \begin{array}{cc} 0 & 1 \\ -1 & 5 \\ \end{array} \right|\\ &=2(38)-4(-7)+3(1) = 107 \end{align*}
Later in this section we will see how determinants are related to area and volume. First, we introduce the cross product, which is defined as a “symbolic” determinant whose first row has the vector entries \(i, j, k\).
CAUTION
Note in Eq.(3) that the middle term comes with a minus sign.
DEFINITION The Cross Product
The cross product of vectors \(\textbf{v}=\langle a_1, b_1,c_1\rangle\) and \(w= \langle a_2, b_2,c_2\rangle\) is the vector \begin{equation} \textbf{v}\times w = \left| \begin{array} i & j & k \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ \end{array} \right| = \left| \begin{array}{cc} b_1 & c_1 \\ b_2 & c_2 \\ \end{array}\right|{i} - \left| \begin{array}{cc} a_1 & c_1 \\ a_2 & c_2 \\ \end{array}\right|{j} + \left| \begin{array}{cc} a_1 & b_1 \\ a_2 & b_2 \\ \end{array}\right|{k}\tag{3} \end{equation}
689
EXAMPLE 2
Calculate \(\textbf{v}\times w\), where \(\textbf{v}=\langle-2,1,4\rangle\) and \(w=\langle 3,2,5\rangle\).
Solution \begin{align*} \textbf{v}\times w &= \left| \begin{array}{rcc} i & j & k \\ -2 & 1 & 4 \\ 3 & 2 & 5 \\ \end{array} \right| = \left| \begin{array}{ccc} 1 & 4 \\ 2 & 5 \\ \end{array} \right|i - \left| \begin{array}{rcc} -2 & 4 \\ 3 & 5 \\ \end{array} \right|j +\left| \begin{array}{rcc} -2 & 1 \\ 3 & 2 \\ \end{array} \right| k \\ &= (-3)i - (-22)j+(-7)k = \langle -3,22,-7\rangle \end{align*}
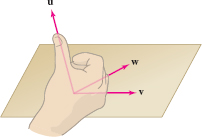
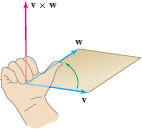
Formula (3) gives no hint of the geometric meaning of the cross product. However, there is a simple way to visualize the vector \(\textbf{v}\times w\) using the right-hand rule. Suppose that \(\textbf{v}\), \(\textbf{w}\), and \(u\) are nonzero vectors that do not all lie in a plane. We say that \(\{v, w, u\}\) forms a right-handed system if the direction of \(u\) is determined by the right-hand rule: When the fingers of your right hand curl from \(\textbf{v}\) to \(\textbf{w}\), your thumb points to the same side of the plane spanned by \(\textbf{v}\) and \(\textbf{w}\) as \(u\) (Figure 12.50). The following theorem is proved at the end of this section.
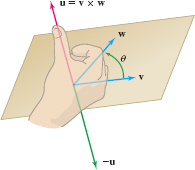
THEOREM 1 Geometric Description of the Cross Product
The cross product \(\textbf{v}\times w\) is the unique vector with the following three properties:
- (i) \(\textbf{v}\times w\) is orthogonal to \(\textbf{v}\) and \(\textbf{w}\).
- (ii) \(\textbf{v}\times w\) has length \(\parallel{v}\ \parallel \parallel{w}\parallel,{\sin\theta}\) (\(\theta\) is the angle between \(\textbf{v}\) and \(\textbf{w}\), \(0\le\theta\le \pi \)).
- (iii) \(\{v, w, v\times w\}\) forms a right-handed system.
How do the three properties in Theorem 1 determine \(\textbf{v}\times w\)? By property (i), \(\textbf{v}\times w\) lies on the line orthogonal to \(\textbf{v}\) and \( w\). By property (ii), \(\textbf{v}\times w\) is one of the two vectors on this line of length \(\parallel{v}\parallel\,\parallel{ w}\parallel\,\sin\theta\). Finally, property (iii) tells us which of these two vectors is \(\textbf{v}\times w\)—namely, the vector for which \(\{v, w, u\}\) is right-handed (Figure 12.51).
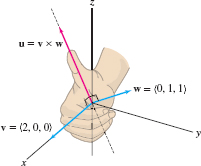
EXAMPLE 3
Let \(\textbf{v}=\langle 2, 0, 0\rangle\) and \( w = \langle 0,1, 1\rangle\). Determine \(u = v\times w\) using the geometric properties of the cross product rather than Eq.(3).
Solution We use Theorem 1. First, by Property (i), \(u= v\times w\) is orthogonal to \(\textbf{v}\) and \( w\). Since \(\textbf{v}\) lies along the \(x\)-axis, \(u\) must lie in the \(yz\)-plane (Figure 12.52). In other words, \(u = \langle 0, b, c\rangle\). But \(u\) is also orthogonal to \( w=\langle 0, 1, 1\rangle\), so \(u\cdot w=b+c=0\) and thus \(u = \langle 0, b, -b\rangle\).
Next, direct computation shows that \(\parallel{v}\parallel=2\) and \(\parallel{w}\parallel = \sqrt 2\). Furthermore, the angle between \(\textbf{v}\) and \( w\) is \(\theta = \frac{\pi}2\) since \(\textbf{v}\cdot w=0\). By property (ii), \[ \parallel{u}\parallel=\sqrt{b^2+(-b)^2}=|b|\sqrt{2} \qquad\textrm{is equal to} \qquad \parallel{v}\parallel \parallel{w}\parallel\sin\frac{\pi}2 = 2\sqrt 2 \]
Therefore, \(|b|=2\) and \(b=\pm 2\). Finally, property (iii) tells us that \(u\) points in the positive \(z\)-direction (Figure 12.52). Thus, \(b=-2\) and \(u = \langle 0, -2, 2\rangle\). You can verify that the formula for the cross product yields the same answer.
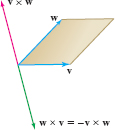
One of the most striking properties of the cross product is that it is anticommutative. Reversing the order changes the sign: \begin{equation} \boxed{ w\times v=- v\times w}\tag{4} \end{equation}
690
We verify this using Eq.(3): when we interchange \(\textbf{v}\) and \(\textbf{w}\), each of the \(2\times 2\) determinants changes sign. For example, \begin{align*} \left| \begin{array}{rcc} a_1 & b_1 \\ a_2 & b_2 \\ \end{array} \right| &= a_1b_2-b_1a_2\\[-6pt] & = -(b_1a_2-a_1b_2) = - \left| \begin{array}{rcc} a_2 & b_2 \\ a_1 & b_1 \\ \end{array} \right| \end{align*}
Anticommutativity also follows from the geometric description of the cross product. By properties (i) and (ii) in Theorem 1, \(\textbf{v}\times w\) and \(w\times v\) are both orthogonal to \(\textbf{v}\) and \(\textbf{w}\) and have the same length. However, \(\textbf{v}\times w\) and \(w\times v\) point in opposite directions by the right-hand rule, and thus \(\textbf{v} \times w=-w \times v\) (Figure 12.53). In particular, \(\textbf{v} \times v=-v \times v\) and hence \(\textbf{v} \times v= 0\).
The next theorem lists some further properties of cross products (the proofs are given as Exercises 45–48.).
Note
Note an important distinction between the dot product and cross product of a vector with itself: \begin{eqnarray*} v \times v &=& \mathbf{0}\\ v \cdot v &=& ||v||^2 \end{eqnarray*}
THEOREM 2 Basic Properties of the Cross Product
- (i) \({w\times v=- v\times w}\)
- (ii) \(\textbf{v}\times v = 0\)
- (iii) \(\textbf{v}\times w = 0\) if and only if \(w = \lambda v\) for some scalar \(\lambda\) or \( v=0\).
- (iv) \({ (\lambda v) \times w = v\times (\lambda w) = \lambda(v\times w)}\)
- (v) \(\begin{array}[t]{rcl} (u+ v)\times w &{}={} & u\times w+ v\times w \\ u\times (v+w) &=& u\times v+u\times w \end{array}\)
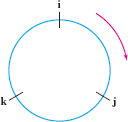
The cross product of any two of the standard basis vectors \(i\), \(j\), and \(k\) is equal to the third, possibly with a minus sign. More precisely (see Exercise 49), \begin{eqnarray} &\displaystyle i\times j= k,\qquad j\times k=i,\qquad k\times i= j \\ &\displaystyle i\times i = j\times j = k\times k =0\tag{5} \end{eqnarray}
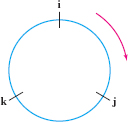
Since the cross product is anticommutative, minus signs occur when the cross products are taken in the opposite order. An easy way to remember these relations is to draw \(i\), \(j\), and \(k\) in a circle as in Figure 12.54. Go around the circle in the clockwise direction (starting at any point) and you obtain one of the relations (5). For example, starting at \(i\) and moving clockwise yields \(i\times j = k\). If you go around in the counterclockwise direction, you obtain the relations with a minus sign. Thus, starting at \(k\) and going counterclockwise gives the relation \( k\times j=-i\).
EXAMPLE 4 Using the \(i j k\) Relations
Compute \((2i+ k)\times (3j+5 k)\).
Solution We use the Distributive Law for cross products: \begin{align*} (2i+ k)\times (3j+5 k) &= (2i)\times (3j)+(2i)\times (5 k)+ k \times (3j)+ k\times (5 k)\\[3pt] &= 6(i \times j) +10(i\times k)+3( k \times j) +5( k\times k)\\[3pt] &= 6 k -10j - 3i +5(v) = -3i-10j+6 k \end{align*}
691
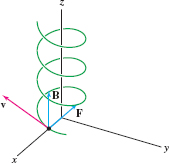
EXAMPLE 5 Velocity in a Magnetic Field
The force \(F\) on a proton moving at velocity \(\textbf{v} \text{m/s}\) in a uniform magnetic field \(B\) (in teslas) is \(F = q( v\times B)\) in newtons, where \(q=1.6\times 10^{-19}\) coulombs (Figure 12.55). Calculate \(F\) if \(B = 0.0004 k\) T and \(\textbf{v}\) has magnitude \(10^6 \text{m/s}\) in the direction \(-j+ k\).
Solution The vector \(-j+ k\) has length \(\sqrt 2\), and since \(\textbf{v}\) has magnitude \(10^6\), \[ \textbf{v} = 10^{6}\left(\frac{- j+ k}{\sqrt 2}\right) \]
Therefore, the force (in newtons) is \begin{align*} F & = q(v\times B)= 10^6q\left(\frac{- j+ k}{\sqrt 2}\right)\times (0.0004 k) = \frac{400q}{\sqrt 2}\left((-j+ k)\times k\right)\\ & = -\frac{400q}{\sqrt 2}i = \frac{-400(1.6\times 10^{-19})}{\sqrt 2}i \approx -(4.5 \times 10^{-17})i \end{align*}
Cross Products, Area, and Volume
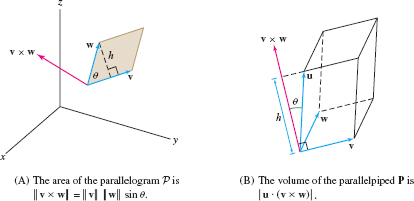
Cross products and determinants are closely related to area and volume. Consider the parallelogram \(\mathcal P\) spanned by nonzero vectors \(\textbf{v}\) and \(\textbf{w}\) with a common basepoint. In Figure 12.56, we see that \(\mathcal P\) has base \(b = \parallel{ v}\) and height \(h = \parallel{w}\sin\theta\), where \(\theta\) is the angle between \(\textbf{v}\) and \(\textbf{w}\). Therefore, \(\mathcal P\) has area \(A = bh = \parallel{ v}\parallel \parallel{w}\parallel\sin\theta =\parallel{v\times w}\parallel\).
Note
A “parallelepiped” is the solid spanned by three vectors. Each face is a parallelogram.
Next, consider the parallelepiped \(\mathbf P\) spanned by three nonzero vectors \(u, v, w\) in \(\textbf{R}^3\) [the three-dimensional prism in Figure 12.56]. The base of \(\mathbf P\) is the parallelogram spanned by \(\textbf{v}\) and \(\textbf{w}\), so the area of the base is \(\parallel{v\times w}\parallel\). The height of \(\mathbf P\) is \(h=\parallel{u}\parallel\cdot|{\cos\theta}|\), where \(\theta\) is the angle between \(u\) and \(\textbf{v}\times w\). Therefore, \[ \textrm{Volume of \(\mathbf P\)} = (\textrm{area of base})(\textrm{height}) = \parallel{ v\times w}\parallel\cdot \parallel{u}\parallel\cdot|{\cos\theta}| \]
But \({\parallel{v\times w}\parallel \parallel{u}\parallel\cos\theta}\) is equal to the dot product of \(\textbf{v}\times w\) and \(u\). This proves the formula \[ \textrm{Volume of \(\mathbf P\)} = |u\cdot (v\times w)| \]
The quantity \(u\cdot (v\times w)\), called the vector triple product, can be expressed as a determinant. Let \[ u=\langle a_1,b_1,c_1\rangle, \qquad v=\langle a_2,b_2,c_2\rangle,\qquad w=\langle a_3,b_3,c_3\rangle \]
692
Then \begin{align} u\cdot(v\times w) & =u\cdot\left(\left| \begin{array}{cc} b_2 & c_2 \\ b_3 & c_3 \\ \end{array}\right|\bf{i} - \left| \begin{array}{cc} a_2 & c_2 \\ a_3 & c_3 \\ \end{array}\right|\bf{j} + \left| \begin{array}{cc} a_2 &b_2 \\ a_3 & b_3 \\ \end{array}\right|\bf{k}\right)\\ &= a_1 \left|\begin{array}{cc} b_2 & c_2 \\ b_3 & c_3 \\ \end{array}\right| - b_1\,\left| \begin{array}{cc} a_2 & c_2 \\ a_3 & c_3 \\ \end{array}\right| + c_1\,\left| \begin{array}{cc} a_2 &b_2 \\ a_3 & b_3 \\ \end{array}\right|\\ &=\left| \begin{array}{ccc} a_1 &b_1 & c_1 \\ a_2 &b_2 & c_2 \\ a_3 &b_3 & c_3 \\ \end{array} \right| =\det\left(\begin{array}{c}u\\ v\\ w \end{array}\right)\tag{6} \end{align}
We obtain the following formulas for area and volume.
Note
We use the following notation for the determinant of the matrix whose rows are the vectors \(\textbf{v}, w, u\): \[ \det\left(\begin{array}{c}u \\ v\\ w \end{array}\right) = \left| \begin{array}{ccc} a_1 &b_1 & c_1 \\ a_2 &b_2 & c_2 \\ a_3 &b_3 & c_3 \\ \end{array} \right| \]
It is awkward to write the absolute value of a determinant in the notation on the right, but we may denote it \[ \left|\det\left(\begin{array}{c}u \\ v\\ w \end{array}\right)\right| \]
THEOREM 3 Area and Volume via Cross Products and Determinants
Let \(u, v, w\) be nonzero vectors in \(\textbf{R}^3\). Then
- (i) The parallelogram \(\mathcal P\) spanned by \(\textbf{v}\) and \(\textbf{w}\) has area \({A = \parallel{v\times w}\parallel}\).
- (ii) The parallelepiped \(\mathbf P\) spanned by \(u\), \(\textbf{v}\), and \(\textbf{w}\) has volume \begin{equation} {V}=|u\cdot (v\times w)| = \left|\det\left(\begin{array}{c} u \\v \\ w \\ \end{array}\right) \right|\tag{7} \end{equation}
EXAMPLE 6
Let \(\textbf{v} = \langle 1, 4, 5\rangle\) and \(w = \langle -2,-1,2\rangle\). Calculate:
- (a) The area \(A\) of the parallelogram spanned by \(\textbf{v}\) and \(\textbf{w}\)
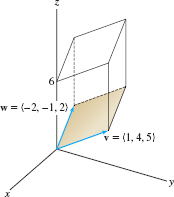
- (b) The volume \(\textbf{v}\) of the parallelepiped in Figure 12.57
Solution We compute the cross product and apply Theorem 3: \[ v\times w = \left|\begin{array}{cc} 4 &5 \\ -1 & 2 \\ \end{array} \right|i - \left|\begin{array}{cc} 1 &5 \\ -2 & 2 \\ \end{array} \right| j + \left|\begin{array}{cc} 1 &4 \\ -2 & -1 \\ \end{array} \right| k = \langle 13, -12,7 \rangle \]
- (a) The area of the parallelogram spanned by \(\textbf{v}\) and \(\textbf{w}\) is \[ A=\parallel{ v\times w}\parallel=\sqrt{13^2+(-12)^2+7^2}=\sqrt{362}\approx 19 \]
- (b) The vertical leg of the parallelepiped is the vector \(6 k\), so by Eq.(7), \[ {V} = |(6 k)\cdot (v\times w)|= |\langle 0,0,6\rangle\cdot \langle 13, -12,7 \rangle| = 6(7)=42 \]
We can compute the area \(A\) of the parallelogram spanned by vectors \(\textbf{v}=\langle a,b\rangle\) and \(w=\langle c, d\rangle\) by regarding \(\textbf{v}\) and \(\textbf{w}\) as vectors in \(\textbf{R}^3\) with zero component in the \(z\)-direction (Figure 12.58). Thus, we write \(\textbf{v}=\langle a,b,0\rangle\) and \(w= \langle c, d, 0\rangle\). The cross product \(\textbf{v}\times w\) is a vector pointing in the \(z\)-direction: \[ v\times w = \left| \begin{array}{rcc} i & j & k \\ a & b & 0 \\ c & d & 0 \\ \end{array} \right| = \left| \begin{array}{ccc} b & 0 \\ d & 0 \\ \end{array} \right|i - \left| \begin{array}{rcc} a & 0 \\ c & 0 \\ \end{array} \right| j +\left| \begin{array}{rcc} a&b \\ c & d \\ \end{array} \right| k = \left| \begin{array}{rcc} a&b \\ c & d \\ \end{array} \right| k \]
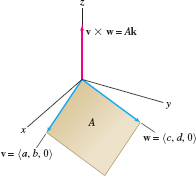
By Theorem 3, the parallelogram spanned by \(\textbf{v}\) and \(\textbf{w}\) has area \(A = \parallel{ v\times w}\parallel\), and thus, \begin{equation} \boxed{A= \left|\det\left(\begin{array}{c} v \\ w \\ \end{array}\right) \right| = \left| \det\left(\begin{array}{cc} a&b\\ c&d \\ \end{array}\right) \right| \vphantom{\dfrac{\arule}{\brule}}}\tag{8} \end{equation}
693
EXAMPLE 7
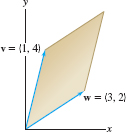
Compute the area \(A\) of the parallelogram in Figure 12.59.
Solution We have \({ \left|\begin{array}{c} v \\ w \\ \end{array} \right| = \left|\begin{array}{cc} 1 &4 \\ 3 & 2 \\ \end{array} \right| = 1\cdot 2 - 3\cdot 4 = -10}\). The area is the absolute value \(A=|-10|=10\).
Proofs of Cross-Product Properties
We now derive the properties of the cross product listed in Theorem 1. Let \[ v = \langle a_1, b_1, c_1\rangle,\qquad w = \langle a_2, b_2, c_2\rangle \]
We prove that \(\textbf{v}\times w\) is orthogonal to \(\textbf{v}\) by showing that \(\textbf{v}\cdot (v\times w) =0\). By Eq.(6), \begin{equation} v\cdot (v\times w) =\det\left(\begin{array}{c} v\\ v\\ w \end{array}\right) = a_1\left|\begin{array}{ccc} b_1 & c_1 \\ b_2 & c_2 \\ \end{array}\right| -b_1\left|\begin{array}{ccc} a_1 & c_1 \\ a_2 & c_2 \\ \end{array}\right| + c_1\left|\begin{array}{ccc} a_1 & b_1 \\ a_2 & b_2 \\ \end{array}\right|\tag{9} \end{equation}
Straightforward algebra (left to the reader) shows that the right-hand side of Ed.(9) is equal to zero. This shows that \(\textbf{v} \cdot (v \times w) = 0\) and thus \(\textbf{v}\times w\) is orthogonal to \(\textbf{v}\) as claimed. Interchanging the roles of \(\textbf{v}\) and \(\textbf{w}\), we conclude also that \(w \times v\) is orthogonal to \(\textbf{w}\), and since \(\textbf{v} \times w = -w \times v\), it follows that \(\textbf{v} \times w\) is orthogonal to \(\textbf{w}\). This proves part (i) of Theorem 1. To prove (ii), we shall use the following identity: \begin{equation}\boxed{ \parallel{ v\times w}\parallel^2=\parallel{ v}\parallel^2\parallel{w}\parallel^2-(v\cdot w)^2}\tag{10} \end{equation}
To verify this identity, we compute \(\parallel{ v\times w}\parallel^2\) as the sum of the squares of the components of \(\textbf{v}\times w\): \begin{align} \parallel{ v\times w}\parallel^2 &= \left|\begin{array}{ccc} b_1 & c_1 \\ b_2 & c_2 \\ \end{array}\right|^2 +\left|\begin{array}{ccc} a_1 & c_1 \\ a_2 & c_2 \\ \end{array}\right|^2 + \left|\begin{array}{ccc} a_1 & b_1 \\ a_2 & b_2 \\ \end{array}\right|^2\notag\\ &=(b_1c_2-c_1b_2)^2+(a_1c_2-c_1a_2)^2+(a_1b_2-b_1a_2)^2\tag{11} \end{align}
On the other hand, by definition, \begin{eqnarray} \parallel{ v}\parallel^2 \parallel{w}\parallel^2-(v\cdot w)^2 =\big(a_1^2+b_1^2+c_1^2\big) \big(a_2^2+b_2^2+c_2^2\big)-(a_1a_2+b_1b_2+c_1c_2)^2\tag{12} \end{eqnarray}
Again, algebra (left to the reader) shows that Eq.(11) is equal to Eq.(12).
Now let \(\theta\) be the angle between \(\textbf{v}\) and \(\textbf{w}\). By Eq.(10), \begin{align*} \parallel{ v\times w}\parallel^2 &=\parallel{v}\parallel^2\parallel{w}\parallel^2-(v\cdot w)^2 =\parallel{v}\parallel^2\parallel{w}\parallel^2-\parallel{v}\parallel^2\parallel{w}\parallel^2\cos^2\theta\\ &=\parallel{v}\parallel^2\parallel{w}\parallel^2(1-\cos^2\theta) =\parallel{v}\parallel^2\parallel{w}\parallel^2\sin^2\theta \end{align*}
Therefore, \({\parallel{v\times w}\parallel =\parallel{v}\parallel{w}\parallel\sin\theta}\). Note that \(\sin\theta\geq 0\) since, by convention, \(\theta\) lies between 0 and \(\pi\). This proves (ii).
Part (iii) of Theorem 1 asserts that \({v, w, v\times w}\) is a right-handed system. This is a more subtle property that cannot be verified by algebra alone. We must rely on the following relation between right-handedness and the sign of the determinant, which can be established using the continuity of determinants: \[ \det\left(\begin{array}{c}u \\ v\\ w \end{array}\right) \gt 0 \quad\textrm{if and only if \({u, v, w}\) is a right-handed system} \]
694
Furthermore, it can be checked directly from Eq.(2) that the determinant does not change when we replace \({u, v, w}\) by \({ v,w,u}\) (or \({w,u, v})\). Granting this and using Eq.(6), we obtain \[ \det\left(\begin{array}{c} v\\ w\\ v\times w \end{array}\right)= \det\left(\begin{array}{c} v\times w \\ v\\ w \end{array}\right) = (v\times w)\cdot(v\times w)=\parallel{ v\times w}\parallel^2>0 \]
Therefore \({v, w, v\times w}\) is right-handed as claimed (Figure 12.60).
12.5.1 Summary
- Determinants of sizes \(2\times 2\) and \(3\times 3\): \begin{eqnarray*} \left| \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array} \right| &=& a_{11}a_{22}-a_{12}a_{21}\\ \left| \begin{array}{ccc} a_{11} & a_{12}&a_{13} \\ a_{21} & a_{22}&a_{23} \\ a_{31} & a_{32}&a_{33} \\ \end{array} \right| &=& a_{11} \left| \begin{array}{cc} a_{22} & a_{23} \\ a_{32} & a_{33} \\ \end{array} \right| -a_{12}\left| \begin{array}{cc} a_{21} & a_{23} \\ a_{31} & a_{33} \\ \end{array} \right| + a_{13}\left| \begin{array}{cc} a_{21} & a_{22} \\ a_{31} & a_{32} \\ \end{array} \right| \end{eqnarray*}
- The cross product of \(\textbf{v}=\langle a_1, b_1, c_1\rangle\) and \(w=\langle a_2, b_2, c_2\rangle\) is the symbolic determinant \[ v\times w = \left| \begin{array}{ccc} i & j & k \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ \end{array} \right| = \left| \begin{array}{cc} b_1 & c_1 \\ b_2 & c_2 \\ \end{array}\right|\bf{i} - \left| \begin{array}{cc} a_1 & c_1 \\ a_2 & c_2 \\ \end{array}\right|\bf{j} + \left| \begin{array}{cc} a_1 & b_1 \\ a_2 & b_2 \\ \end{array}\right|\bf{k} \]
- The cross product \(\textbf{v}\times w\) is the unique vector with
the following three properties:
- (i) \(\textbf{v}\times w\) is orthogonal to \(\textbf{v}\) and \(\textbf{w}\).
- (ii) \(\textbf{v}\times w\) has length \(\parallel{v}\parallel \parallel{w}\parallel\sin\theta\) (\(\theta\) is the angle between \(\textbf{v}\) and \(w, 0 \le \theta \le \pi)\).
- (iii) \({v, w, v\times w}\) is a right-handed system.
- Properties of the cross product:
- (i) \(w\times v=- v\times w\)
- (ii) \(\textbf{v}\times w=0\) if and only if \(w = \lambda v\) for some scalar or \(\textbf{v}= 0\)
- (iii)] \({ (\lambda v) \times w = v\times (\lambda w) = \lambda(v\times w)}\)
- (iv) \(\begin{array}[t]{rcl} (u+ v)\times w &{}={}& u\times w+ v\times w \\ v\times (u+w) &=& v\times u+ v\times w \\ \end{array}\)
- Cross products of standard basis vectors (Figure 12.61): \[ i\times j = k,\qquad j\times k = i,\qquad k\times i = j \]
- The parallelogram spanned by \(\textbf{v}\) and \(\textbf{w}\) has area \(\parallel{v\times w}\parallel\).
- Cross-product identity: \({\parallel{v\times w}\parallel^2=\parallel{ v}\parallel^2\parallel{w}\parallel^2-(v\cdot w)^2}\).
- The vector triple product is defined by \(u\cdot (v\times w)\). We have \[ u\cdot (v\times w) = \det\left(\begin{array}{c} u\\ v\\ w \\ \end{array}\right) \]
- The parallelepiped spanned by \(u\), \(\textbf{v}\), and \(w\) has volume \(|u\cdot (v\times w)|\) .
695